
 Image credit: Mark Avara
Image credit: Mark Avara
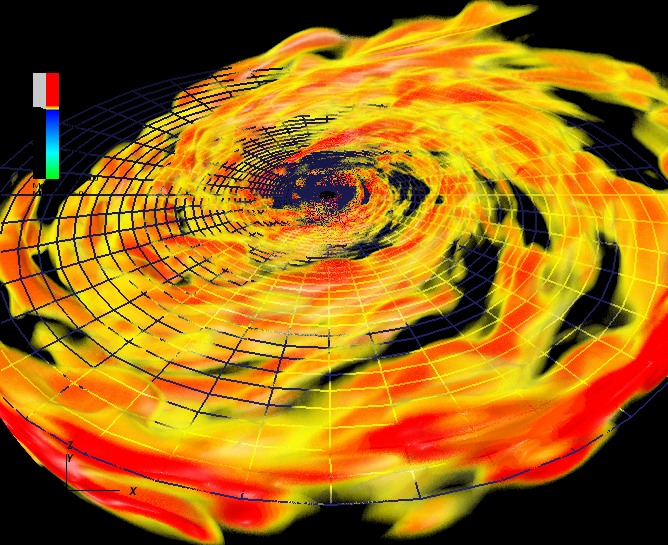
Theoretical astrophysics has long relied on numerical simulations as a formidable way to improve our understanding of the dynamics of astrophysical systems. Fortunately, the mathematical framework upon which such simulations are based is developed to high levels of sophistication. The equations governing the dynamics of relativistic astrophysical systems are an intricate set of coupled, time-dependent partial differential equations, comprising the general relativistic hydrodynamics and magnetohydrodynamics equations and Einstein’s gravitational field equations.
CCRG members have developed significant expertise to handle such systems and there are a number of long-term and ambitious projects dedicated to this area. Our main general relativistic and magneto-hydrodynamics project involves the accretion of magnetized gas onto one or more supermassive black holes, and to explore associated relativistic phenomena such as jets in active galactic nuclei. Jets and disks can produce kilonovea events.
A kilonova is a transient astronomical event that emits electromagnetic radiation from radioactive decay when the merger of binary black holes or neutron stars. In 2017, The LIGO scientific collaboration found evidence that two neutron stars merged, which produced gravitational waves, a gamma-ray burst, and a kilonova. This event is widely hailed as the start of multi-messenger astronomy. In addition to this, CCRG researchers use combined general relativistic and magneto-hydrodynamics simulations are also used to model black hole - neutron star and neutron star - neutron star binaries. These astrophysical sources are believed to be the origin of gamma ray bursts.
Radiative transfer describes how energy is transferred through electromagnetic radiation. Absorption emission and scattering processes all describe how the electromagnetic wave travels through a medium, and are included radiative transfer equation. For the most simplistic cases, analytic solutions can be found, but for more complicated systems numerical techniques must be employed to describe the system.










