Abstract

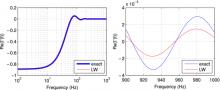
Searches for gravitational waves with km-scale laser interferometers often involve the long-wavelength approximation to describe the detector response. The prevailing assumption is that the corrections to the detector response due to its finite size are small and the errors due to the long-wavelength approximation are negligible. Recently, however, Baskaran and Grishchuk (2004 Class. Quantum Grav. 21 4041) found that in a simple Michelson interferometer such errors can be as large as 10%. For more accurate analysis, these authors proposed to use a linear-frequency correction to the long-wavelength approximation. In this paper we revisit these calculations. We show that the linear-frequency correction is inadequate for certain locations in the sky and therefore accurate analysis requires taking into account the exact formula, commonly derived from the photon round-trip propagation time. Also, we extend the calculations to include the effect of Fabry–Perot resonators in the interferometer arms. Here we show that a simple approximation which combines the long-wavelength Michelson response with the single-pole approximation to the Fabry–Perot transfer function produces rather accurate results. In particular, the difference between the exact and the approximate formulae is at most 2–3% for those locations in the sky where the detector response is greater than half of its maximum value. We analyse the impact of such errors on detection sensitivity and parameter estimation in searches for periodic gravitational waves emitted by a known pulsar, and in searches for an isotropic stochastic gravitational-wave background. At frequencies up to 1 kHz, the effect of such errors is at most 1–2%. For higher frequencies, or if more accuracy is required, one should use the exact formula for the detector response.