Abstract

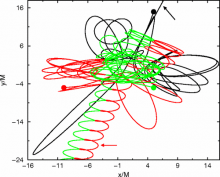
We present techniques for long-term, stable, and accurate evolutions of multiple-black-hole spacetimes using the `moving puncture' approach with fourth- and eighth-order finite difference stencils. We use these techniques to explore configurations of three black holes in a hierarchical system consisting of a third black hole approaching a quasi-circular black-hole binary, and find that, depending on the size of the binary, the resulting encounter may lead to a prompt merger of all three black holes, production of a highly elliptical binary (with the third black hole remaining unbound), or disruption of the binary (leading to three free black holes). We also analyze the classical Burrau three-body problem using full numerical evolutions. In both cases, we find behaviors distinctly different from Newtonian predictions, which has important implications for N-body black-hole simulations. For our simulations we use analytic approximate data. We find that the eighth-order stencils significantly reduce the numerical errors for our choice of grid sizes, and that the approximate initial data produces the expected waveforms (after a rescaling of the puncture masses) for black-hole binaries with modest initial separations