Abstract
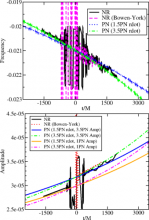
We explore how a recently developed analytical black-hole binary spacetime can be extended using numerical simulations to go beyond the slow-inspiral phase. The analytic spacetime solves the Einstein field equations approximately, with the approximation error becoming progressively smaller the more separated the binary. To continue the spacetime beyond the slow-inspiral phase, we need to transition. Such a transition was previously explored at smaller separations. Here, we perform this transition at a separation of D=20M (large enough that the analytical metric is expected to be accurate), and evolve for six orbits. We find that small constraint violations can have large dynamical effects, but these can be removed by using a constraint-damping system like the conformal covariant formulation of the Z4 system. We find agreement between the subsequent numerical spacetime and the predictions of post-Newtonian theory for the waveform and inspiral rate that is within the post-Newtonian truncation error.