Abstract

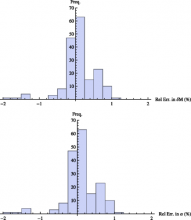
We perform a set of 38 numerical simulations of equal-mass BH binaries in a configuration where the BH spins in the binary are equal in both magnitude and direction, to study precession effects. We vary the initial direction of the total spin S with respect to the orbital angular momentum L, covering the 2 dimensional space of orientation angles with 38 configurations consisting of 36 configurations distributed in the azimuthal angle phi and polar angle theta, and two configurations on the poles. In all cases, we set the initial dimensionless BH spins to 0.8. We observe that during the late-inspiral stage, the total angular momentum of the system J remains within 5 deg of its original direction, with the largest changes in direction occurring when the spins are nearly counter-aligned with the orbital angular momentum. We also observe that the angle between S and L is nearly conserved during the inspiral phase. These two dynamical properties allow us to propose a new phenomenological formula for the final mass and spin of merged BHs in terms of the individual masses and spins of the progenitor binary at far separations. We determine coefficients of this formula (in the equal-mass limit) using a least-squares fit to the results of this new set of 38 runs, an additional set of five new configurations with spins aligned/counteraligned with the orbital angular momentum, and over 100 recent simulations. We find that our formulas reproduce the remnant mass and spin of these simulations to within a relative error of 2.5%. We discuss the region of validity of this dynamical picture for precessing unequal-mass binaries. Finally, we perform a statistical study to see the consequence of this new formula for distributions of spin-magnitudes and remnant masses with applications to BH-spin distributions and gravitational radiation in cosmological scenarios involving several mergers.