Abstract

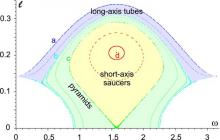
We discuss the properties of orbits within the influence sphere of a supermassive black hole (BH), in the case that the surrounding star cluster is nonaxisymmetric.  There are four major orbit families; one of these, the pyramid orbits, have the interesting property that they can approach arbitrarily closely to the BH.  We derive the orbit-averaged equations of motion and show that in the limit of weak triaxiality, the pyramid orbits are integrable: the motion consists of a two-dimensional libration of the major axis of the orbit about the short axis of the triaxial figure, with eccentricity varying as a function of the two orientation angles, and reaching unity at the corners.  Because pyramid orbits occupy the lowest angular momentum regions of phase space, they compete with collisional loss cone repopulation and with resonant relaxation in supplying matter to BHs.  We derive expressions for the capture rate, including the effects of general relativistic precession which imposes an upper limit to the eccentricity.  We show that capture from pyramid orbits can dominate the feeding of BHs, particularly in giant galaxies, at least until such a time as the pyramid orbits are depleted; however this time can be of order a Hubble time.  Our results provide new insight into the mechanism of resonant relaxation, particularly as it applies to very eccentric orbits.