Analytic solution of the SEIR epidemic model via asymptotic approximant
Published in Physica D: Nonlinear Phenomena, 132633
(Thursday, June 25, 2020)
Abstract
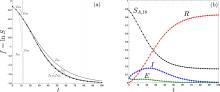
An analytic solution is obtained to the SEIR Epidemic Model. The solution is created by constructing a single second-order nonlinear differential equation in lnS and analytically continuing its divergent power series solution such that it matches the correct long-time exponential damping of the epidemic model. This is achieved through an asymptotic approximant (Barlow et al., 2017) in the form of a modified symmetric Padé approximant that incorporates this damping. The utility of the analytical form is demonstrated through its application to the COVID-19 pandemic.