Abstract

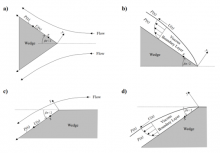
We demonstrate that the asymptotic approximant applied to the Blasius boundary layer flow over a flat plat (Barlow et al., 2017 Q. J. Mech. Appl. Math., 70(1): 21-48) yields accurate analytic closed-form solutions to the Falkner-Skan boundary layer equation for flow over a wedge having angle βπ/2 to the horizontal. A wide range of wedge angles satisfying β∈[−0.198837735,1] are considered, and the previously established non-unique solutions for β<0 having positive and negative shear rates along the wedge are accurately represented. The approximant is used to determine the singularities in the complex plane that prescribe the radius of convergence of the power series solution to the Falkner-Skan equation. An attractive feature of the approximant is that it may be constructed quickly by recursion compared with traditional Padé approximants that require a matrix inversion. The accuracy of the approximant is verified by numerical solutions, and benchmark numerical values are obtained that characterize the asymptotic behavior of the Falkner-Skan solution at large distances from the wedge.