Abstract
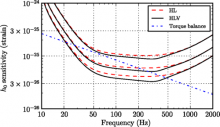
We consider the cross-correlation search for periodic gravitational waves and its potential application to the low-mass x-ray binary Sco X-1. This method coherently combines data not only from different detectors at the same time, but also data taken at different times from the same or different detectors. By adjusting the maximum allowed time offset between a pair of data segments to be coherently combined, one can tune the method to trade off sensitivity and computing costs. In particular, the detectable signal amplitude scales as the inverse fourth root of this coherence time. The improvement in amplitude sensitivity for a search with a maximum time offset of one hour, compared with a directed stochastic background search with 0.25-Hz-wide bins, is about a factor of 5.4. We show that a search of one year of data from the Advanced LIGO and Advanced Virgo detectors with a coherence time of one hour would be able to detect gravitational waves from Sco X-1 at the level predicted by torque balance over a range of signal frequencies from 30 to 300 Hz; if the coherence time could be increased to ten hours, the range would be 20 to 500 Hz. In addition, we consider several technical aspects of the cross-correlation method: We quantify the effects of spectral leakage and show that nearly rectangular windows still lead to the most sensitive search. We produce an explicit parameter-space metric for the cross-correlation search, in general, and as applied to a neutron star in a circular binary system. We consider the effects of using a signal template averaged over unknown amplitude parameters: The quantity to which the search is sensitive is a given function of the intrinsic signal amplitude and the inclination of the neutron-star rotation axis to the line of sight, and the peak of the expected detection statistic is systematically offset from the true signal parameters. Finally, we describe the potential loss of signal-to-noise ratio due to unmodeled effects such as signal phase acceleration within the Fourier transform time scale and gradual evolution of the spin frequency.