Abstract

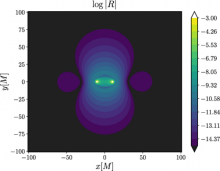
We construct an approximate metric that represents the spacetime of spinning binary black holes (BBH) approaching merger. We build the metric as an analytical superposition of two Kerr metrics in harmonic coordinates, where we transform each black hole term with time-dependent boosts describing an inspiral trajectory. The velocities and trajectories of the boost are obtained by solving the post-Newtonian (PN) equations of motion at 3.5 PN order. We analyze the spacetime scalars of the new metric and we show that it is an accurate approximation of Einstein's field equations in vacuum for a BBH system in the inspiral regime. Furthermore, to prove the effectiveness of our approach, we test the metric in the context of a 3D general relativistic magneto-hydrodynamical (GRMHD) simulation of accreting mini-disks around the black holes. We compare our results with a previous well-tested spacetime construction based on the asymptotic matching method. We conclude that our new spacetime is well-suited for long-term GRMHD simulations of spinning binary black holes on their way to the merger.