Abstract

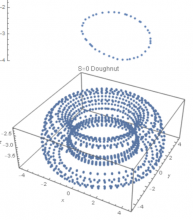
We revisit the definition of transverse frames and tetrad choices with regards to its application to numerically generated spacetimes, in particular those from the merger of binary black holes. We introduce the concept of local and approximate algebraic Petrov types in the strong field regime. We define an index D=12/I−−−−√(Ψ2−Ψ23/Ψ4) able to discriminate between Petrov types II and D and define regions of spacetime of those approximate types when used in conjunction with the speciality invariant S=27J2/I3. We provide an explicit example applying this method to Brill-Lindquist initial data corresponding to two nonspinning black holes from rest at a given initial separation. We find a doughnut-like region that is approximately of Petrov type II surrounded by an approximately Petrov type D region. We complete the study by proposing a totally symmetric tetrad fixing of the transverse frame that can be simply implemented in numerically generated spacetimes through the computation of spin coefficients ratios. We provide an application by explicitly deriving the Kerr-perturbative equations in this tetrad.