Abstract

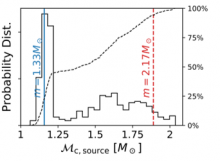
Observations of the properties of multiple coalescing neutron stars will simultaneously provide insight into neutron star mass and spin distribution, the neutron star merger rate, and the nuclear equation of state. Not all merging binaries containing neutron stars are expected to be identical. Plausible sources of diversity in these coalescing binaries can arise from a broad or multi-peaked NS mass distribution; the effect of different and extreme NS natal spins; the possibility of NS-BH mergers; or even the possibility of phase transitions, allowing for NS with similar mass but strongly divergent radius. In this work, we provide a concrete algorithm to combine all information obtained from GW measurements into a joint constraint on the NS merger rate, the distribution of NS properties, and the nuclear equation of state. Using a concrete example, we show how biased mass distribution inferences can significantly impact the recovered equation of state, even in the small-N limit. With the same concrete example, we show how small-N observations could identify a bimodal mass and spin distribution for merging NS simultaneously with the EOS. Our concordance approach can be immediately generalized to incorporate other observational constraints.