Abstract
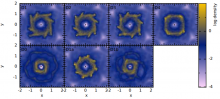
The equations of smoothed particle magnetohydrodynamics (SPMHD), even with the various corrections to instabilities so far proposed, have been observed to be unstable when a very steep density gradient is necessarily combined with a variable smoothing length formalism. Here we consider in more detail the modifications made to the SPMHD equations in LBP2015 that resolve this instability by replacing the smoothing length in the induction and anisotropic force equations with an average smoothing length term. We then explore the choice of average used and compare the effects on a test `cylinder-in-a-box' problem and the collapse of a magnetised molecular cloud core. We find that, aside from some benign numerical effects at low resolutions for the quadratic mean, the formalism is robust as to the choice of average but that in complicated models it is essential to apply the average to both equations; in particular, all four averages considered exhibit similar conservation properties. This improved formalism allows for arbitrarily small sink particles and field geometries to be explored, vastly expanding the range of astronomical problems that can be modeled using SPMHD.