Abstract

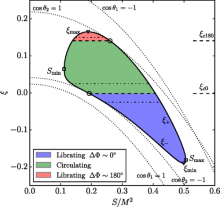
We derive an effective potential for binary black hole (BBH) spin precession at second post-Newtonian order. This effective potential allows us to solve the orbit-averaged spin-precession equations analytically for arbitrary mass ratios and spins. These solutions are quasiperiodic functions of time: after a fixed period, the BBH spins return to their initial relative orientations and jointly precess about the total angular momentum by a fixed angle. Using these solutions, we classify BBH spin precession into three distinct morphologies between which BBHs can transition during their inspiral. We also derive a precession-averaged evolution equation for the total angular momentum that can be integrated on the radiation-reaction time and identify a new class of spin-orbit resonances that can tilt the direction of the total angular momentum during the inspiral. Our new results will help efforts to model and interpret gravitational waves from generic BBH mergers and predict the distributions of final spins and gravitational recoils.