Abstract
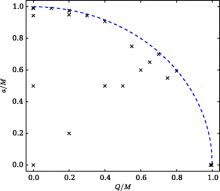
The nonlinear stability of Kerr-Newman black holes (KNBHs) is investigated by performing numerical simulations within the full Einstein-Maxwell theory. We take as initial data a KNBH with mass M, angular momentum to mass ratio a and charge Q. Evolutions are performed to scan this parameter space within the intervals 0≤a/M≤0.994 and 0≤Q/M≤0.996, corresponding to an extremality parameter a/amax (amax≡√M2−Q2) ranging from 0 to 0.995. These KNBHs are evolved, together with a small bar-mode perturbation, up to a time of order 120M. Our results suggest that for small Q/a, the quadrupolar oscillation modes depend solely on a/amax, a universality also apparent in previous perturbative studies in the regime of small rotation. Using as a stability criterion the absence of significant relative variations in the horizon areal radius and BH spin, we find no evidence for any developing instability.