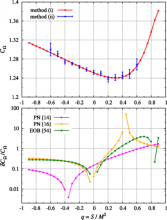
Abstract
For a self-gravitating particle of mass \mu in orbit around a Kerr black hole of mass M >> \mu, we compute the O(\mu/M) shift in the frequency of the innermost stable circular equatorial orbit (ISCEO) due to the conservative piece of the gravitational self-force acting on the particle. Our treatment is based on a Hamiltonian formulation of the dynamics in terms of geodesic motion in a certain locally-defined effective smooth spacetime. We recover the same result using the so-called first law of binary black-hole mechanics. We give numerical results for the ISCEO frequency shift as a function of the black hole's spin amplitude, and compare with predictions based on the post-Newtonian approximation and the effective one-body model. Our results provide an accurate strong-field benchmark for spin effects in the general relativistic two-body problem.