Abstract

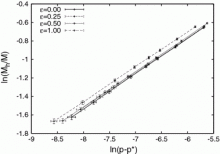
We investigate non-spherically symmetric, scalar field collapse of a family of initial data consisting of a spherically symmetric profile with a deformation proportional to the real part of the spherical harmonic Y21(θ,φ). Independent of the strength of the anisotropy in the data, we find that supercritical collapse yields a black hole mass scaling Mh∝(p−p∗)γ with γ≈0.37, a value remarkably close to the critical exponent obtained by Choptuik in his pioneering study in spherical symmetry. We also find hints of discrete self-similarity. However, the collapse experiments are not sufficiently close to the critical solution to unequivocally claim that the detected periodicity is from critical collapse echoing.