Abstract

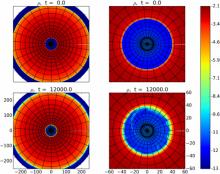
We present a new warped gridding scheme adapted to simulate gas dynamics in binary black hole spacetimes. The grid concentrates grid points in the vicinity of each black hole to resolve the smaller scale structures there, and rarefies grid points away from each black hole to keep the overall problem size at a practical level. In this respect, our system can be thought of as a "double" version of the fisheye coordinate system, used before in numerical relativity codes for evolving binary black holes. The gridding scheme is constructed as a mapping between a uniform coordinate system--in which the equations of motion are solved--to the distorted system representing the spatial locations of our grid points. Since we are motivated to eventually use this system for circumbinary disk calculations, we demonstrate how the distorted system can be constructed to asymptote to the typical spherical polar coordinate system, amenable for efficiently simulating orbiting gas flows about central objects with little numerical diffusion. We discuss its implementation in the Harm3D code, tailored to evolve the magnetohydrodynamics (MHD) equations in curved spacetimes. We evaluate the performance of the system's implementation in Harm3D with a series of tests, such as the advected magnetic field loop test, magnetized Bondi accretion, and evolutions of hydrodynamic disks about a single black hole and about a binary black hole. Like we have done with Harm3D, this gridding scheme can be implemented in other unigrid codes as a (possibly) simpler alternative to adaptive mesh refinement (AMR).