Abstract

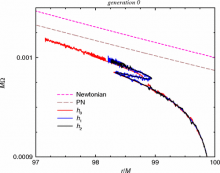
We perform several black-hole binary evolutions using fully nonlinear numerical relativity techniques at separations large enough that low-order post-Newtonian expansions are expected to be accurate. As a case study, we evolve an equal-mass nonspinning black-hole binary from a quasicircular orbit at an initial coordinate separation of D=100M for three different resolutions. We find that the orbital period of this binary (in the numerical coordinates) is T=6422M. The orbital motion agrees with post-Newtonian predictions to within 1%. However, we find that the time derivative of the coordinate separation is dominated by a purely gauge effect leading to an apparent contraction and expansion of the orbit at twice the orbital frequency. Based on these results, we improved our evolution techniques and studied a set of black hole binaries in quasicircular orbits starting at D=20M, D=50M, and D=100M for ∼5, 3, and 2 orbits, respectively. We then find good agreement between the numerical results and post-Newtonian predictions for the orbital frequency and radial decay rate, radiated energy and angular momentum, and waveform amplitude and phases. The results are relevant for the future computation of long-term waveforms to assist in the detection and analysis of gravitational waves by the next generation of detectors as well as the long-term simulations of black-hole binaries required to accurately model astrophysically realistic circumbinary accretion disks.