Abstract

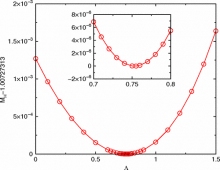
We study conformally-flat initial data for an arbitrary number of spinning black holes with exact analytic solutions to the momentum constraints constructed from a linear combination of the classical Bowen-York and conformal Kerr extrinsic curvatures. The solution leading to the largest intrinsic spin, relative to the ADM mass of the spacetime epsilon_S=S/M^2_{ADM}, is a superposition with relative weights of Lambda=0.783 for conformal Kerr and (1-Lambda)=0.217 for Bowen-York. In addition, we measure the spin relative to the initial horizon mass M_{H_0}, and find that the quantity chi=S/M_{H_0}^2 reaches a maximum of \chi^{max}=0.9856 for Lambda=0.753. After equilibration, the final black-hole spin should lie in the interval 0.9324<chi_{final}<0.9856. We perform full numerical evolutions to compute the energy radiated and the final horizon mass and spin. We find that the black hole settles to a final spin of chi_{final}^{max}=0.935 when Lambda=0.783. We also study the evolution of the apparent horizon structure of this "maximal" black hole in detail.