Abstract
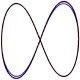
There are periodic solutions to the equal-mass three-body (and N-body) problem in Newtonian gravity. The figure-eight solution is one of them. In this paper, we discuss its solution in the first and second post-Newtonian approximations to General Relativity. To do so we derive the canonical equations of motion in the ADM gauge from the three-body Hamiltonian. We then integrate those equations numerically, showing that quantities such as the energy, linear and angular momenta are conserved down to numerical error. We also study the scaling of the initial parameters with the physical size of the triple system. In this way we can assess when general relativistic results are important and we determine that this occur for distances of the order of 100M, with M the total mass of the system. For distances much closer than those, presumably the system would completely collapse due to gravitational radiation. This sets up a natural cut-off to Newtonian N-body simulations. The method can also be used to dynamically provide initial parameters for subsequent full nonlinear numerical simulations.